数组：逻辑概念 / 二分查找 / 冒泡排序 / 快速排序 / 复杂度·源栈课堂·一起帮

数组：逻辑概念 / 二分查找 / 冒泡排序 / 快速排序 / 复杂度

“逻辑”概念

复习：

数据结构是一个“逻辑”概念
要拿到数据，必须知道它的地址

以数组为例，在大多数语言中（C#/Java）中：

数组就是一排连续的盒子
每一个盒子都有一个地址，获取盒子里的数据（元素）需要知道它的地址
但数组这排盒子的地址是连续的，或者说，这一排盒子占用了一段连续的地址
所以我们只需要记录第一个盒子的地址（存储在数组变量名中）
当我们要取第n个盒子里的数据，只需要在第一个盒子的地址上加n，就能直接得到该盒子的地址

注意上面第4条，这是我们理解数组的关键，这也是数组被如此广泛使用的原因：我们不是从数组中第1个元素开始，依次挨着数（找）第2个第3个……直到第n个，而是通过运算直接得到第n个数组元素的地址！所以，取数组中第2000个元素，并不会比取数组中第2个元素慢。

但在JavaScript中，数组的底层实现不是这样的，它实际上采用哈希表和链表的方式，存储数组元素。@想一想@：为什么？

飞哥推测（为什么是推测？/捂脸.jpg：语言本身只定义语法，不管底层实现）是因为JavaScript弱/动态类型的原因。

但不管底层是如何实现，只要一个东东，能让我们从0开始按下标存取数据，它就是数组。（领会：逻辑概念）

数组一般又可分为：

静态/定长数组：如C#/Java，一旦初始化就确定长度，一旦确定无法更改
动态/变长数组：如JavaScript，长度可以随时变……

之后继续会学：还有一维/二维/交错……数组

冒泡排序

需求：将数组中的数字（比如：9 2 3 5 4 7 6 8 1 0），按从小到大的顺序排列

PS：憋说你一眼就看出来啦……

建议：在学习冒泡排序之前，先@想一想@自己的方案，比如，可不可以：

PS：读别人的代码，比自己写还难

准备一个同样大小的空数组（以下称为：结果数组）
原数组中找到一个最大值（max），放到结果数组第1位
~~原数组中删除这个最大值（不行，做不到）~~，改成：在原数组中找到除了max以下最大（第2大）的，放到结果数组第2位
循环上述过程，在原数组中找到第3大的，放到结果数组第3位
……

然后，对比一下最经典的入门级算法：冒泡排序

PPT动画演示：

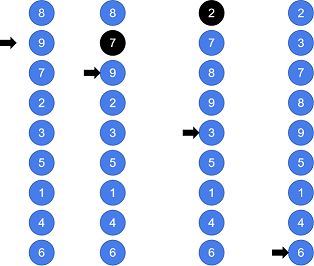
其核心就是：

遍历数组
相邻两个元素交换
两个循环：一个从上往下，一个从下往上

光说不练假把式！上代码：

//从小到大
for(let i=0; i<arr.length-1; i++){
	if(arr[i] > arr[i+1]){
		for(let j=i+1; j>0; j--){    //j从大到小了
			if(arr[j] < arr[j-1]){
				//交换数组元素
				let temp = arr[j];
				arr[j] = arr[j-1];	
				arr[j-1] = temp;	
			}else{
				break;    //注意：提高性能！
			}
		}
	} //else nothing
}

二分查找

猜数字的游戏（1-1000），你会怎么猜？

500：大了
250：小了
350：小了
400：大了
375：小了
385：你特么真是个天才！

其实，你这种猜测方法，归纳出来就是二分查找法。

将数组中间位置的元素与查找值比较，如果两者相等，则查找成功；
否则利用中间位置记录将数组分成前、后两个集合，
- 如果中间位置元素大于查找值，则进一步在其左边/前面的元素中查找，
- 否则在其右边/后面的元素中查找
重复以上过程，直到找到满足条件的元素

以下代码演示：

先准备一个数组：不要忘了前提：数组元素有有序排列的
```
let arr = [3, 8, 7, 12, 23, 35, 46, 59, 70, 108];
```

用一个变量target来表示要查找的值

let target = 8;  
//也可以给一个数组中不存在的值，比如72 
//找不到  -1

引入左右指针是关键：把被我们人脑“脑补”出来的东西（所谓的中间下标是怎么来的？）给代码补上
```
let left = 0,
	right =  arr.length,
	i = Math.floor((left+right)/2);
```

开始循环，通过left/right值的改变确定每一次循环是i的值（注意：代码有错误且不完全）

while(target!=arr[i]){    //是这样的吗？

	if(target > arr[i]){
		//改left还是right？怎么改
	}else if(target < arr[i]){
		//是不是类似于：left = ？
	}else{  //找到了
		//找到	index
		return i; //?
	}
	
	//可以和循环前的i赋值合并么？
	i = Math.floor((left + right)/2);
}

快速排序

月薪18K的算法，^_^

先上PPT演示：

总结：

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小
然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行……
直到：整个数据变成有序序列。

第一轮

为什么不能简单的按照上述描述进行coding？

受限于“数组”的特征：定长定位。没有int[-1]啊！数组的操作只有一个：交换（swap）

#悟#：运动是相对的。

所以，衍生出来如下方法：（PPT演示）

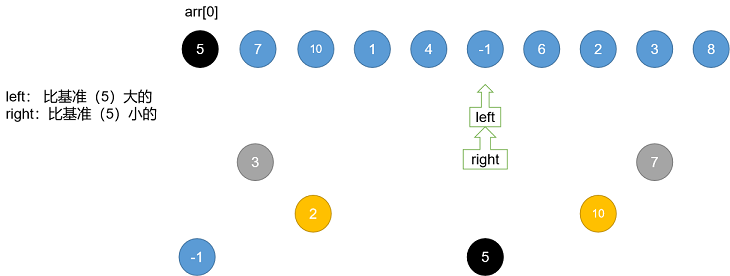
其核心步骤包括：

选定一个基数（通常就是数组第一个数）
设定一个左指针，一个右指针。程序运行之后，
- 左指针从左往右移动
- 右指针从右往左移动
记忆：一个基数两个指针，^_^
从左往右找到比基数大的数A，从右往左找比基数小的数B：交换A和B
重复第2/3步，直到直到左右指针重合，指向最后一个终点值（飞哥自命名）这时候：
- 左边都是比基数小的数
- 右边都是比基数大的数
将基数和终点值比较，如果：
- 终点值比基数小，直接交换；
- 否则，将基数和终点值前一位数交换

演示代码：

let arr = [18, 7, 5, 9, 12, 23, 16, 32, 1, 3];

let i = 0,
	left = 1,
	right = arr.length-1;

while(left<right){    //循环条件
	while(arr[left]<arr[i]){
		if(left==right){
			break;
		}
		left++;	//一直加到 arr[left]>=arr[i];
	}
	//停下来，准备交换
	
	while(arr[right]>arr[i]){
		if(left==right){
			break;
		}		
		right--;
	}
	
	if(left == right){    //如果左右指针已经重合
		if(arr[left]>arr[i]){
			swap(arr, left-1, i);
		}else{
			swap(arr, left, i);
		}
	}else{
		swap(arr, left, right);
		left++;
		right--;		
	}
}

递归调用

完成一轮排序之后，如何对其左右两部分再进行一次排序呢？而且还要将这个过程一直执行下去呢……

童鞋们，这就是典型的递归啊！

首先，将每一轮的排序抽象成方法：

function quickSort(arr, left, right){    //@想一想@：为什么要left和right参数？

#小技巧#：记录下每一轮排序前的oldLeft和oldRight：

let oldLeft = left, oldRight = right;

一轮排序完成之后，继续调用方法自己：（@想一想@：middle是啥，从哪里来？）

//左边排序
quickSort(arr, oldLeft, middle - 1);

//右边排序
quickSort(arr, middle + 1, oldRight);

特别注意，一定要想好递归结束的条件：

if (left >= right)
{	
	return;
}

复杂度

@想一想@：冒泡排序和快速排序哪一个更快？为什么呢？

我们使用复杂度来衡量一个（比较各个）算法的效率：

空间复杂度 S(n)

还记得飞哥自创的排序法不？用一个新数组按从小到大的顺序来装原数组……这种算法，就额外耗费了一个数组的存储空间；

而冒泡排序法，只耗费了多少额外空间？一个元素对应的临时变量而已。

这种算法所需的额外存储空间多少，就是空间复杂度。

时间复杂度 O(n)

按字面意思，是指完成某个算法需要消耗的时间。

但因为耗时受硬件影响，不够客观，我们我们通常以运算（循环）次数衡量。

PS：理解不同语义下的“复杂”：执行 v.s. 设计

同时，算法还受数据影响

可能有最好的情况（比如第一次循环就找到），
还有可能有最坏的情况（比如直到循环结束才找到），
我们一般默认指的是通常状况，或者说算法的平均复杂度。

用大O表示，指示所需运算（循环）次数和参与运算元素之间的关系，一般包括三个量级：

线性：O(n），类似于 y=x
指数：O(n^2)，类似于 y=x^2
对数：O(log(n))，类似于 y=log(x)

@想一想@：冒泡和快速排序，遍历和二分查找的复杂度。

闲话

为什么是：数据结构和算法，而不是算法和数据结构呢？揭示：

算法依赖于数据结构。

@想一想@：能举一个例子么？

作业

改造冒泡排序：
1. 让结果从大到小排序
2. 将其封装成方法bubbleSort()，且该方法既能按元素本身大小比较，也能按元素的绝对值（即：数组中可能有负数）进行比较
3. 可以指定数组中的某一个值为最大（就像斗地主有“癞子”一样）
完成二分查找法，将其封装成函数/方法：BinarySeek()
修复课堂中快排的bug，用更优雅的方式实现，提示：
1. left-1有无可能为负数？
2. 数组以18开头试试
3. 能不能减少while嵌套（使用continue）
4. 最后和基数的交换能不能放到while之外
5. ……
PS：一定要自己思考自己调试，这是学习数算的一个重要目的！
彻底完成快速排序！冲击月薪18K，^_^